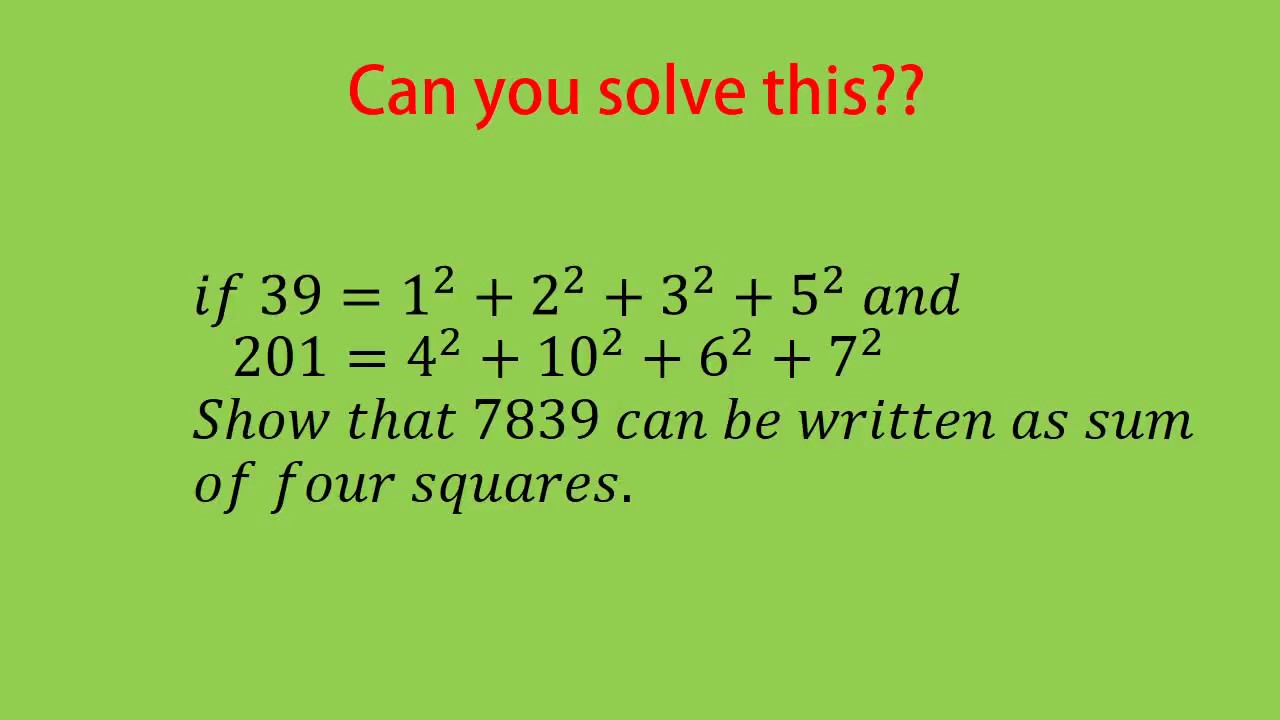Casa
four square theorem

PDF] New parametrization of $A^2+B^2+C^2=3D^2$ and Lagrange's four-square theorem

Por um escritor misterioso

Descrição
In this paper we provide a new parametrization for the diophantine equation $A^2+B^2+C^2=3D^2$ and give a series of corollaries. We discuss some connections with Lagrange's four-square theorem. As applications, we find new parameterizations of equilateral triangles and regular tetrahedrons having integer coordinates in three dimensions.
PDF] New parametrization of $A^2+B^2+C^2=3D^2$ and Lagrange's four-square theorem
PDF) Using Quaternions for Parametrizing 3-D Rotations in
PDF] New parametrization of $A^2+B^2+C^2=3D^2$ and Lagrange's four-square theorem
Efficient optimization with higher-order ising machines
PDF] New parametrization of $A^2+B^2+C^2=3D^2$ and Lagrange's four-square theorem
Axioms, Free Full-Text
PDF] New parametrization of $A^2+B^2+C^2=3D^2$ and Lagrange's four-square theorem
Frontiers Parameterization modeling for wind drift factor in oil
PDF] New parametrization of $A^2+B^2+C^2=3D^2$ and Lagrange's four-square theorem
Applied Sciences, Free Full-Text
PDF] New parametrization of $A^2+B^2+C^2=3D^2$ and Lagrange's four-square theorem
Energies, Free Full-Text
PDF] New parametrization of $A^2+B^2+C^2=3D^2$ and Lagrange's four-square theorem
Lagrangian
PDF] New parametrization of $A^2+B^2+C^2=3D^2$ and Lagrange's four-square theorem
2020 preTEST5A
PDF] New parametrization of $A^2+B^2+C^2=3D^2$ and Lagrange's four-square theorem
Lagrange's Four-Square Theorem, PDF, Number Theory
de por adulto (o preço varia de acordo com o tamanho do grupo)